Today I’m going to cover the basics of AC circuits, how they differ from DC circuits which I covered previously. Again there’s going to be a bunch of math, please don’t get hung up on details. If you’re confused by something roll forward and see if there’s something that helps clear it up. If not, ask a question. The math is merely a tool to help explain what’s going on, don’t get lost in it.
A side note from as I wrote this, I forgot how complicated a lot of this stuff is. Seriously, most of the stuff on this page I don’t even give a second though and trying to remember how to explain it isn’t easy. I have a heavy math background and it’s simple for me, though I know it won’t be for everyone. I have no doubt someone’s going to get confused, seriously ask questions, please.
What is AC
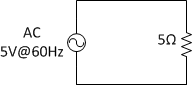
The difference between AC and DC is how the current flows through the wire. In a DC circuit voltage is constant and as a result the current will be constant as well. AC on the other hand cycles back and forth at a particular frequency. This cyclical action reacts with two of the three passive components previously discussed in a peculiar manner. To make things simple we’ll start with a simple AC circuit.
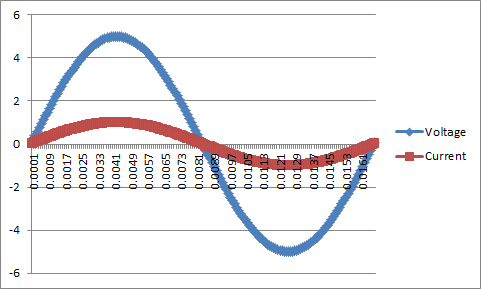
An AC source is simply described mathematically as a sine wave. Given the circuit as described we can find the current flowing through it at any time.
For those who can’t visualize what’s going on, here’s a graph.
Remember the relationship between voltage and current in a simple resistor circuit is linear so the current is always proportional to the voltage. Now though we’re gong to talk about the two other components that react a bit differently.
Reactance and Impedance
Capacitors and inductors if you remember resist changes in voltage and current respectively. We now are applying a voltage however that is constantly changing. Now is where we discover a different type of resistance called Reactance.
Reactance is frequency dependent and describes how the component will react within the circuit. It provides us with the information to find the phase relationship, as well define the current/voltage relationship at any point in time. Reactance and resistance combine together to provide us an impedance. This impedance helps provide a complete definition for the circuit. First though we will discuss reactance from Capacitors and Inductors.
Reactance of Capacitors
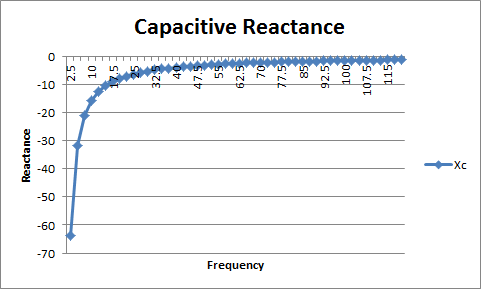
Capacitors at low frequencies look like an open circuit since no current flows through them. This is because at low frequencies the circuit almost looks most like DC. While at high frequencies the capacitor appears to be a short circuit. This is because a capacitor’s reactance is inversely proportional to the frequency.
Here’s a plot of reactance for a small capacitor, you can see it decreases as the frequency increases. For now ignore the sign, that will be discussed when Impedance is covered.
Reactance of Inductors
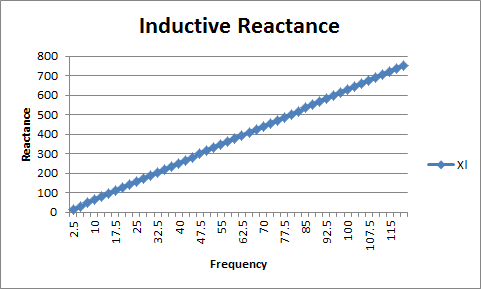
Inductors are the opposite of capacitors if your remember, and their reactance shows it. At low frequencies the inductor appears to be a short circuit. This is because the current isn’t really changing that fast so the magnetic field is quite stable. This means that at high frequencies though the inductor appears to be an open circuit. So while a capacitor is inversely proportional, an inductor is just proportional to the frequency.
Here’s the same plot as above but for an inductor.
Impedance
The reason you didn’t need to worry about the sign is it doesn’t really matter until you want to know what has happened to the current. Both of these items cause current to shift in time by an offset or “angle”.
Finding the overall Impedance is actually quite simple, the why of this is a bit more complicated and is an entire post in itself. The simplest statement is it is a result of effect the component has on the current voltage relationship. To start with though impedance is found through the following equation.
This relationship allows us to find the phase relationship between current and voltage based off the reactance. This is where that sign difference between the inductor and capacitor comes into play. The (-) on the capacitive reactance equation means that the current will “lag” the voltage by 90 degrees if there is no other resistance within the circuit. The imaginary values provide us a second axis to explain the relationship.
Remember one cycle is 360 degrees or 2π, so if we shift the current it can be measured from the relative 0. This leads us to phasor representation. We can display the two axes together with just an angle and a magnitude. I’m not going to go through all the details for phasors or what all can be done with them.
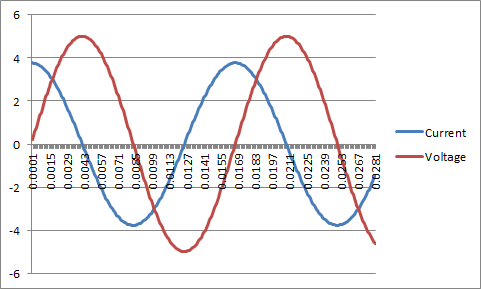
Here is an example AC circuit with only a capacitor:
The reactance and impedance can be found by doing the following:
Here’s a plot of a similar circuit with an inductor for comparison.
Why You Care
Impedance is a very important concept since it is required to help describe what is happening within a system. This lead and lag concept and why it is important will become more obvious as we begin to start discussing power.
Power Basics
Power is simply the rate at which you are doing work. In classical physics it is force times velocity. Within the circuit however we can find the power being used by a component or being delivered to the system quite easily. The power equation is defined as follows:
Given this we can also perform a substitution using Ohm’s law and find that the following also describes the power consumed by an element:
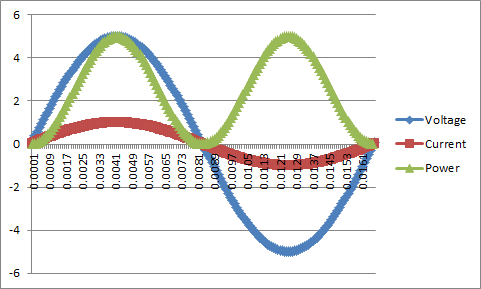
Previously it was shown how long wires can have very large resistances and that the voltage is stepped up for moving power long distances. The above is why. Since power is directly related to the voltage and current, it is much more efficient to have a much lower power loss caused by the wire. Moving forward though we have the following graph of a simple AC circuit with current, voltage, and now a third line, power.
Notice how the power is pulsing. This pulsing action is problematic for applications where you need a smooth and constant application of power. This also creates a problem on the generator that can be quickly discussed. Power can also be defined as the following:
A product of torque and angular velocity. Now imagine that you’re turning a crank trying to lift a bucket from the bottom of a well. If as you were cranking up the bucket at the top and bottom of the crank absolutely no force was required, not only that but the bucket didn’t move while there. When pulling mid crank however the bucket moved quite quickly but it also required more force from you to pull. All the while the rotational speed of you spinning the crank remained the same. It would be very difficult, and from a mechanical standpoint it can cause vibration through the system.
To solve this issue we generate and distribute in what’s called three phase power. Instead of supplying a single voltage and current we supply three, 120 degrees apart. The total power being generated/delivered is the sum of all three.
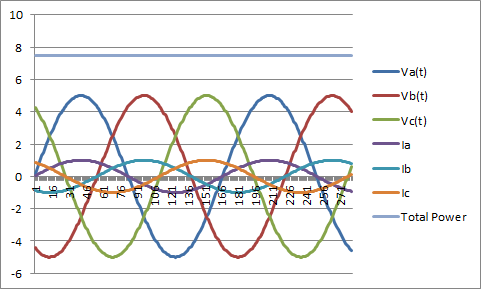
Using that same sample circuit modified into a three phase system we get the following graph.
Notice the total power is dead flat, the three phase generator is always putting out the same amount of power. The reasoning behind why this works will be discussed in the next article that talks about synchronous generation.
What About Real Loads
So far my examples in the power section have only involved purely resistive loads where there is no impedance from capacitors or inductors. In the real world though every type of load also provides some impedance that alters the phase relationship between current and voltage.
There are actually two types of power in the electrical system. There first is real power, and is described as power actually consumed by the load. The second is reactive power, this is power that is not consumed by the load but ends up in purgatory between the load and source. These two are sometimes combined to create apparent power, which describes what appears to be supplied to the load according to the generator.
Mathematically it is described as follows:
The phase relationship between current and voltage leads to something called Power Factor or P.F. It simply describes the weight between real and reactive power. PF is found by the following:
Ideally you want a PF of 1 meaning the system is entirely in phase. The reason for this is that a utility can only bill for Real power, they cannot charge you for reactive or apparent power. Many companies with highly capacitive or inductive loads try to work this to their advantage. The result is that the utility then bills them considerably more for the power they are using. It is stressful to the system and is basically trying to cheat it. The problem is easily solved by adding capacitor or inductor banks to even out the impedance of the load.
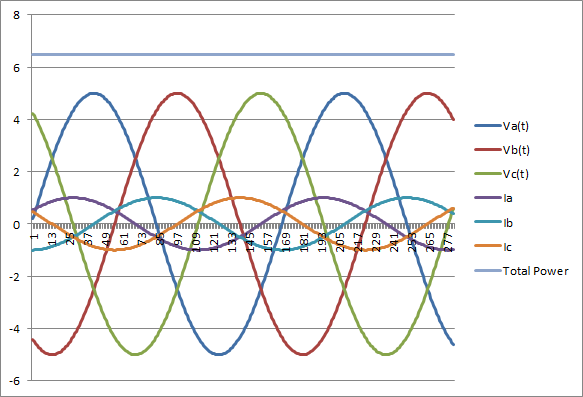
Let’s look at what happens to our power if we let our PF slip to say 30 degrees and why it’s such a problem. This is the same exact 3 phase system shown above but the currents have been shifted by 30 degrees.
Notice the power delivered has decreased, this is because the current and voltages are no longer reaching their peaks simultaneously. Instead the power delivered is equivalent to the original power multiplied by the power factor.
Review:
So there was a quick run down on impedance, calculating power, why we have 3 phase power, and what happens when we combine it all together. Next week I’m going to talk about synchronous machines, how they work, and the basics of generation involving them.
TMM is the owner, editor, and principal author at The Minuteman, a competitive shooter, and staff member for Boomershoot. Even in his free time he’s merging his love and knowledge of computers and technology with his love of firearms.
Many know his private name and information however due to the current political climate, many are distancing themselves due to the abandonment of Due Process.









Nothing specific, just wanted to note I appreciate the work you’re putting into this series.
It’s bringing back a lot of stuff I haven’t really had to use since I graduated. For the most part I just touch everything conceptually now since most everything I work with detail wise is in software.
I’m amazed at how much I still retain, but even more so how much I’m grabbing my textbooks to suck out the details. 3 years ago I could have rattled most everything I’ve done thus far without even a second though.
As my dad said though if you want to thoroughly understand something, teach it while using it. So far that’s holding quite true.
Pingback: We Need More Power! - The Minuteman